自旋霍爾效應
 | |
| 圖一:霍爾效應示意圖: (a) 傳統霍爾效應; (b) 自旋霍爾效應。 | |
若在通電流的導體上外加橫向磁場,電荷載子在勞倫茲 (Lorentz) 力的作用下會往垂直於電流方向的兩邊偏移[如圖一(a)所示],造成導體兩側有電壓降。這個1879年美國學者Edwin Hall發現的現象叫做霍爾(Hall)效應。1970年代初,兩位蘇聯學者Dyakonov和Perel指出即使沒有外加磁場,由於相對論自旋—軌道耦合效應,自旋向上的載子受雜質散射後會往一邊偏移而自旋向下的載子會往另一邊偏移 [稱扭轉(skew)散射或莫特(Mott) 散射],形成自旋流[如圖一(b)所示]。這種現象稱為自旋霍爾效應(spin Hall effect)。最近,日本Murakami等人[1]提出在块材半導體或二維自由電子系統中,即使沒有雜質散射,由於相對論對能帶的影響,也會出現自旋霍爾效應。這種自旋霍爾效應,被稱為內在(intrinsic)自旋霍爾效應,以便和Dyakonov和Perel的自旋霍爾效應區隔,後者被稱為外在(extrinsic)自旋霍爾效應。和傳統霍爾效應及量子霍爾效應不同,而且無需外加磁場。也就是說,人們可利用自旋霍爾效應在非磁性材料如半導體上,無外加磁場的情況下,產生自旋流。人們可以利用現代高度發達的半導體技術,研制完全電驅動的自旋電子學裝置。因此,在自旋電子學熱的今天,自旋霍爾效應最近引起世界各地學者的熱烈討論與研究。 | |
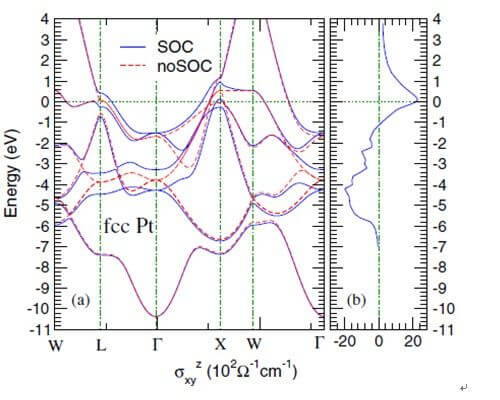 | |
| 圖二:鉑的相對論’電子能帶結構(a)和自旋霍爾電導率(b)[4]。 | |
半導體中的自旋霍爾效應是在低温下觀察到的。最近,多位實驗學者如日本Otani等人發現有些金属(如鉑Pt)在室温下亦出現很大的自旋霍爾效應[2],但別的金属如鋁和銅的自旋霍爾效應則很小[2,3]。自旋霍爾效應和金属本身有很大的關聯,顯示內在機制可能起重要作用。我們利用第一原理方法計算了鉑和鋁的內在自旋霍爾效應,發現鉑在低温下有巨大的自旋霍爾電導[ 高達~2200 ( ħ /e )(Ωcm)-1 ],在室温下自旋霍爾電導仍有~240 ( ħ /e )(Ωcm)-1 [4],與實驗吻合。我們還應用Berry相位理論計算了每條能帶與每個k-點對自旋霍爾電導的貢獻,發現這巨大的自旋霍爾效應主要來自費米能級附近因自旋-軌道耦合而劈裂的原簡并的d-軌道能帶 [如圖三中L和X高對稱點附近的能帶]。這些劈裂的能帶對自旋霍爾電導的貢獻巨大但符號相反。所以,當費米能級落在自旋-軌道耦合劈裂的能隙時,這種材料就會呈現巨大的自旋霍爾效應。鋁和金的費米能級落在自旋-軌道耦合較小的s/p-軌道能帶上,因而自旋霍爾效應較小[4,5]。 令人稱奇的是,日本實驗學者Seki等人在金里亦觀察到龐大的自旋霍爾效應,比鉑還大兩個數量級[6]。顯然,這龐大的自旋霍爾效應不可能是金的內在自旋霍爾效應造成的[5]。那么這龐大的自旋霍爾效應由何而來呢?我們經了解實驗樣品的制備過程,覺得金樣品可能含有鐵、鉑和金空穴等雜質。這些雜質對導電電子的散射都有可能造成龐大的自旋霍爾效應。我們於是研究金中金空穴、鉑和鐵等雜質的電子態[7],我們的LDA+U計算顯示鐵雜質具有磁矩且其態密度出現大的自旋劈裂,自旋向下的態密度有一尖峰落在費米能級(圖三)。因此,我們提出在鐵雜質在金系统里,可能發生了有趣的多d-軌道關聯近藤效應。eg-軌道處在近藤极限其近藤溫度極低(液態氦溫度),而t2g-軌道處於混價態區域其近藤溫度應高於室溫。因而在室溫下,t2g-軌道可能造成共振扭轉散射(圖一),產生龐大的自旋霍爾效應[7]。 我們進一步在玻恩近似下估算雜質扭轉散射的自旋霍爾角(γs),得到自旋霍爾角約為0.1,與實驗結果[6] 大致相同。這個理論不但能解釋金中龐大的自旋霍爾效應,而且為這個被研究數拾年的古典近藤系统引進新的話題。物理評論通訊的主編認為這篇論文[15]是數拾年來對近藤問題的重要貢献,特地邀請美國近藤效應專家P. Coleman教授為這一研究成果做專欄評論[8]。然而,我們的多軌道近藤效應模型在理論上受到挑戰。Costi等學者認為鐵雜質在金系统里應該屬於單純的三簡並通道近藤模型,其基態的軌道磁矩應為零[9],與我們LDA+U+SOI計算結果[7]不符。在實驗上,X光磁雙向色性(magnetic circular dichroism) 方法量測到的鐵雜質的軌道磁矩很小[10],似乎亦與我們計算結果[7]有矛盾。 | |
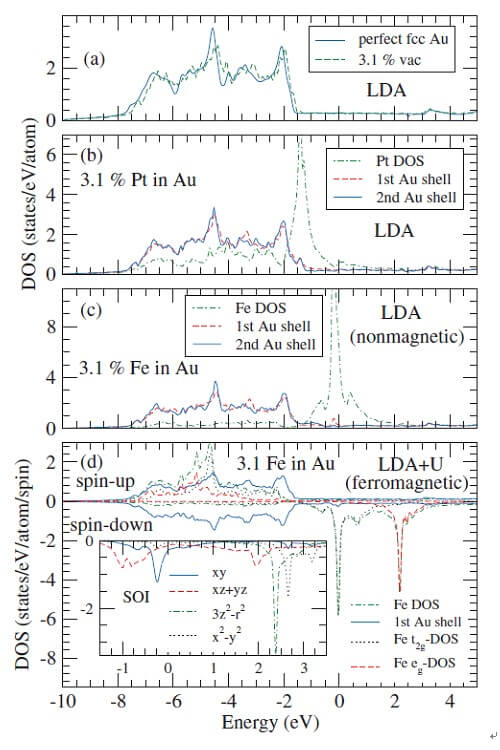 | |
| 圖三:(a) 純金與含3.1%空穴的金, (b) 含3.1%鉑雜質的金, (c) 含3.1%鐵雜質的金的電子態密度 [7]。 | |
我們認為這些差別可能是由在近藤溫度下強烈的量子漲落造成的,而第一原理計算是沒有包含量子漲落的。所以,我們最近先利用第一原理計算建立了描述鐵雜質-金系统的真實的(realistic)多軌道安德森(Anderson)模型,然后應用量子蒙特卡羅(Monte Carlo)模擬研究這個安德森模型的多軌道近藤效應[11]。我們的量子蒙特卡羅模擬証實鐵雜質的eg-軌道呈現傳统的低温(~1K)近藤效應,而t2g-軌道則顯示高於室温的近藤效應。更有趣的是,量子蒙特卡羅模擬結果還顯示:d-電子的關聯性(U)和強烈的量子漲落重整(renormalize)或增強了自旋-軌道的關聯(lzσz) (圖四),從而產生了龐大的自旋霍爾效應。利用量子蒙特卡羅模擬結果和扭轉散射公式(1) 的計算顯示鐵雜質在金系统里的自旋霍爾角高達0.06[11],接近實驗值[6],証明多軌道近藤效應和量子漲落得确會產生實驗學者觀察到的龐大的自旋霍爾效應。 | |
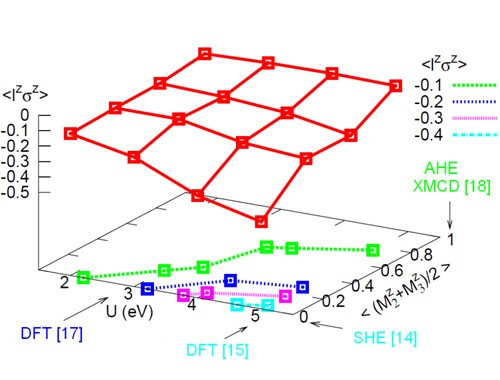 | |
圖四:含鐵雜質塊材金系统的量子蒙特卡羅模擬結果:自旋-軌道的關聯(lzσz)與多體關聯能U和自旋磁化M的相圖[13]。模擬溫度為360 K,自旋-軌道耦合強度λ為75 meV。 | |
最後,我們考慮外加磁場。我們進一步的量子蒙特卡羅模擬結果顯示外加磁場雖然產生自旋磁化但大大削減了量子漲落和自旋-軌道的關聯(lzσz) (圖四),這就解釋了之前的X光磁雙向色性實驗為什麼沒有量測到大軌道磁矩[10]。X光磁雙向色性實驗需要加磁場讓樣品磁化。 | |
參考文獻
| |
